故事 #
昨天從家裡翻出舊書《葛老爹的推理遊戲 1》
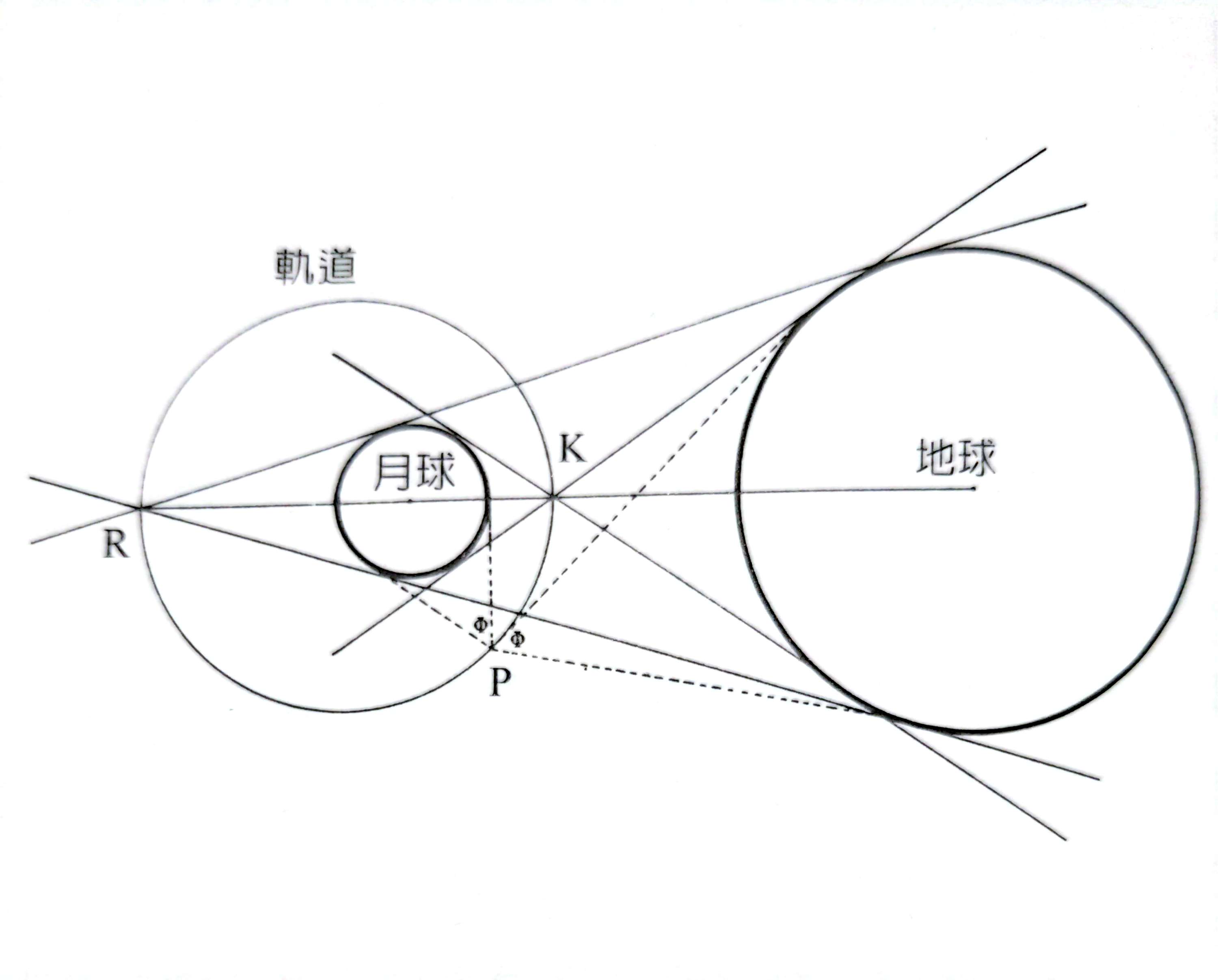
過地心和月心的某平面上,有一軌道,其上任一處觀測地球和月亮,兩者視覺大小相同。
問:軌道的形狀?
答:圓形。
軌道為圓的證明 #
設地月半徑比為 m:e,則有 月P:P地 = 月K:K地 = 月R:R地 = m:e
即 ∠地P月 之內分角線為 PK;外分角線為 PR
故 ∠KPR = 90°;P 在直徑 KR 的圓周上
這對幾何能力不佳的我來說不太直覺。應該有什麼投影方式,可以說「以軌道為鏡,月球的像和地球重疊」。且「物、鏡、像三者組合中,知其二就能決定第三者」。
總覺得高中時的我應該有一套解釋!現在卻想不起來……
相關知識 #
我怕自己越忘越多,所以趕快記錄一下還知道的。
反演 #
今天在維基上看到的一種映射。把點 P 對圓 O 反演到點 P’。有 O、P、P’ 共線,且 OP * OP’ = r^2。
我玩了一下 desmos,仍想不出化圓為圓的用處。
雙極座標 #
這個維基條目意外地陌生。從國中到大學微積分,課本好像都只有教直(斜)角座標和極座標,沒有用過雙極座標。
平面雙極座標有原點 O 和參考點 R,點 P 的座標為 (∠OPR, OP/PR) 。座標網格線正交。

- 我視力不好,大學時在教室選座位,都要儘可能最大化黑板或投影幕的視覺大小。此時黑板兩側為 O, R,坐位是 P。我進每間教室都會在心裡畫 OPR 的等角圈圈,決定要座前排角落還是後排中間。
- OP/PR 的用途我沒遇過。或許在大金屬版上,有一熱源點和一散熱點時,OP/PR 會是等溫圈。等溫線呈圓形,對熱脹冷縮來說應該是好事。
- 座標網格線正交,可能可以拿來當 special case 驗證某些定理吧。
雙極座標系統好像有很多種有用的對偶方式,值得細想。
結論 #
我實在想不起來高中時學阿波羅圓是做什麼的……